Spectral modelling
HySimCaR (Kuester 2011, Kuester et al. 2014, Spengler 2014) is a spectral, spatial and temporal simulation for modelling the spectral reflectance and BRDF (bidirectional reflectance function) of different cereal canopies. This was realised by an integration of detailed virtual 3D cereal canopies of different growth stages, whose geometries were linked with corresponding spectral information. This system enables the simulation of realistic reflectance spectra on the basis of virtual 3D scenarios incorporating any possible viewing position.
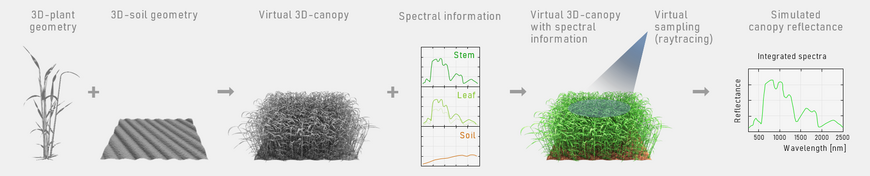
The 4D plant models, such as those for barley shown in the figure above, were developed with the scientific plant modeling system AmapSim (Barczi et al. 2008), a scientific software based on botanical theory. Each plant is described by areas (leaves) and cylinders (stems and ears). The underlying soil surface is modelled by in-situ measured height profiles. The plant positions are determined by the 3D soil surface entering the number of plants per meter and row. The canopy consists of several 3D plants cloned and superposed on the 3D soil surface. Each clone is randomly twisted around itself and placed on the calculated position. The development of the plant models is based on a detailed study of the geometrical appearance and growth stages. Therefore, numerous features describing the plant's shape were collected in the field
The simulation process requires information about optical material properties in terms of reflectance and transmittance of each plant organ (stem, leaf, and ear). The data are measured with an ASD FieldSpec Pro in the spectral range of 350 nm – 2500 nm. The figure schematically visualizes the generation of a 3D scenario, its virtual sampling, and the resulting product, the integrated spectrum of the virtual vegetation canopy. The canopy reflectance is calculated by the aDvanced Radiometric rAy Tracer (drat, on GitHub as librat), an efficient Monte-Carlo ray tracing renderer (Lewis 1999). The resulting canopy reflectance data is determined by the acquisition and illumination geometry as well as the geometry and spectral information of the objects on the surface.
Reflectance Anisotropy
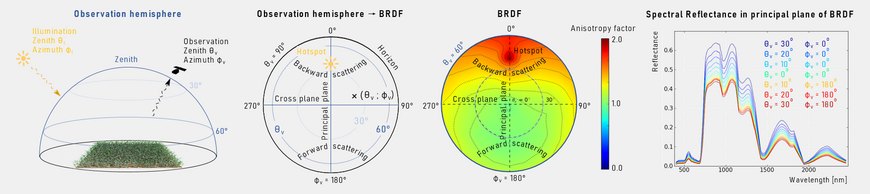
Canopy bidirectional reflectance (BRDF, bidirectional reflectance function) is determined by the interactions between the incoming solar radiation and the plants within the canopy, which depends on the optical and structural properties of the vegetation, the underlying soil, and the illumination and viewing geometry. In order to understand BRDF-influenced reflectance signals, this influence must be identified and quantified, which requires detailed knowledge of the structure and BRDF of the observed vegetation canopies. The figure shows the BRDF effect in a cereal field, once photographed with the illumination in the back (left photo, backward scattering) and once photographed against the illumination (right photo). The different contrast and intensity in the photos caused by backward and forward scattering are clearly visible.
Another important challenge is the acquisition and analysis of realistic BRDF data, since a direct measurement of the BRDF, that is wavelength dependent, is not possible. Instead, numerous individual reflectance measurements from different observation positions are necessary, which are distributed over the entire observation hemisphere of the canopy in order to approximate the BRDF. In-situ BRDF measurements are time consuming and depend on the availability of a field goniometer. In contrast to field measurements, computer-aided simulations offer an alternative approach in which parameter-controlled scenarios of virtual 3D vegetation canopies are virtually sampled under constant illumination conditions. HySimCaR enables the simulation of realistic reflectance spectra on the basis of virtual 3D scenarios and Monte-Carlo raytracing incorporating any possible viewing position. The figure visualizes the relationship between the observation hemisphere above a surface and the BRDF of a surface. The principal plane of the BRDF, the plane along which the strongest anisotropy occurs, always results from the azimuth direction of the illumination source. The azimuth angle of the BRDF thus always corresponds to the relative azimuth angle between the illumination direction and the observation direction (see Kuester & Spengler 2018).
Applications
Modeling sparse vegetation scenarios of agricultural land for analyzing the impact of vegetation cover on soil spectral features. The simulation system HySimCaR (hyperspectral simulation of canopy reflectance) is used to generate virtual agricultural field scenarios differing in type of coverage, fractional cover and soil background. The varying range in fractional cover is determined by varying field structure, plant numbers and geometries, for scenarios associated with early green phenological stages or with dry residues after harvest. The field structure of the early green phenological stages can be varied through row distance, the number of plants and their phenological stage. The field structure of the after harvest scenarios with the dry residues can be varied through row distance and the number of vertical and horizontal residues (see Kuester et al. 2018).
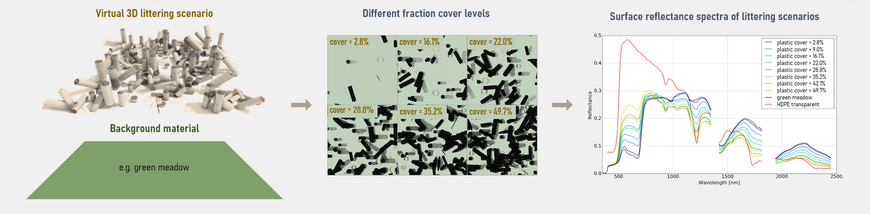
Modeling of plastic littering scenarios for analyzing the detectability and identifiability of different plastic materials in the terrestrial environment. Here the HySimCaR model was used to generate a simulated spectral data base of various terrestrial plastic littering scenarios to investigate the potential, challenges and limits for plastic identification and mapping using hyperspectral remote sensing technique. A data base of different plastic littering scenarios varying in plastic object shapes, plastic material, degree of coverage, and different underlying background spectral properties has been generated (see Kuester & Bochow 2019).
References
J-F Barczi, H Rey, Y Caraglio, P de Reffye, D Barthélémy, Q X Dong and T Fourcaud (2008). AmapSim: A structural whole-plant simulator based on botanical knowledge and designed to host external functional models. Annals of Botany, 101, 1125-1138.
P Lewis (1999). Three-dimensional plant modelling for remote sensing simulation studies using the botanical plant modelling system. Agronomie, 19, 185-210.
Publications
T Kuester & M Bochow (2019): Spectral Modeling of Plastic Litter in Terrestrial Environments - Use of 3D Hyperspectral Ray Tracing Models to Analyze the Spectral Influence of Different Natural Ground Surfaces on Remote Sensing Based Plastic Mapping - Papers, Whispers 2019 - 10th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Amsterdam, The Netherlands, 2019.
T Kuester, S Chabrillat, D Spengler, K Ward, S Förster (2018): Quantifying and Correcting the Impact of Vegetation Cover on Soil Spectral Features Based on Simulated Cereal Canopy Reflectance Spectra - Papers, Whispers 2018 - 9th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Amsterdam, The Netherlands, 2018.
T Kuester & D Spengler (2018): Structural and Spectral Analysis of Cereal Canopy Reflectance and Reflectance Anisotropy. Remote Sensing, 10, 1767.
T Kuester, D Spengler, J-F Barczi, K Segl, P Hostert, H Kaufmann (2014): Simulation of Multitemporal and Hyperspectral Vegetation Canopy Bidirectional Reflectance Using Detailed Virtual 3-D Canopy Models. - IEEE Transactions on Geoscience and Remote Sensing, 52, 4, p. 2096-2108.
D Spengler (2014): Charakterisierung von Getreidearten aus hyperspektralen Fernerkundungsdaten auf der Basis von 4D-Bestandsmodellen, PhD Thesis, Technische Universität Berlin, Fakultät VI - Planen Bauen Umwelt.
D Spengler, T Kuester, A Frick, D Scheffler, H Kaufmann (2013): Correcting the influence of vegetation on surface soil moisture indices by using hyperspectral artificial 3D-canopy models - Proceedings of SPIE, Image and Signal Processing for Remote Sensing XV, 88870Y, SPIE Remote Sensing Conference (Dresden 2013) (Dresden 2013).
T Kuester (2011): Modellierung von Getreidebestandsspektren zur Korrektur BRDF-bedingter Einflüsse auf Vegetationsindizes im Rahmen der EnMAP-Mission, PhD Thesis, Humboldt Universität zu Berlin, Mathematisch-Naturwissenschaftliche Fakultät II.